个人网页
0%

机器学习数学笔记-分类

发表于 更新于

感知机

感知机是一种监督学习算法，用于解决线性可分（Linearly Separable）的二分类问题，具体内容如下：

计算预测值：$z=w_1x_1 + w_2x_2 + b$

激活函数为阶跃函数：

$$ y_{pred}= \begin{cases} 1 & z \ge 0\\ 0 & z \lt 0 \end{cases} $$

参数更新函数：

$$ w_i = w_i + \eta \cdot (y_{true} - y_{pred}) \cdot x_i$$
$$b = b + \eta \cdot (y_{true} - y_{pred})$$

下面我们通过具体的例子，应用一下上面的公式来使用感受一下：

学生有两门课程的成绩，语文和数学，预测是否通过考试

假设每科分数均为 0-100，同时总分超过 120 分为通过考试

构造测试数据

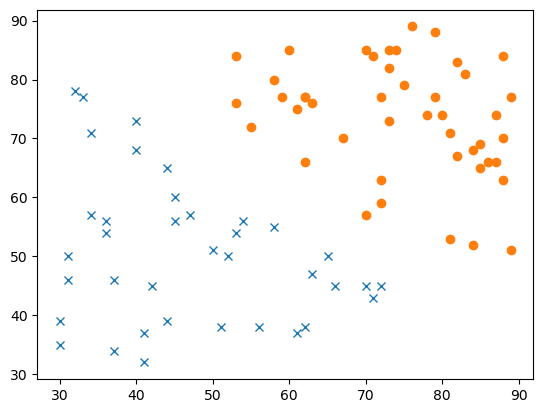
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

num_samples = 50

# 随机生成50个两科的成绩分数（分值在 30-80）
X_1 = np.random.randint(30, 80, size=(num_samples, 2))
# 找出其中两科总和小于120的学生，为 未通过的成绩
X_fail = X_1[(X_1[:, 0] + X_1[:, 1] < 120)]

# 随机生成50个两科的成绩分数（分值在 50-90）
X_2 = np.random.randint(50, 90, size=(num_samples, 2))
# 找出其中两科总和大于120的学生，为 通过的成绩
X_pass = X_2[(X_2[:, 0] + X_2[:, 1] >= 120)]

# 将两类数据合并
train_x = np.vstack([X_fail, X_pass])
# 生成对应的标签(通过为 1，未通过为 0)
train_y = np.array([0] * len(X_fail) + [1] * len(X_pass))

# 未通过的成绩点用 x 表示
plt.plot(train_x[train_y == 0][:, 0], train_x[train_y == 0][:, 1], 'x')
# 通过的成绩点用 o 表示
plt.plot(train_x[train_y == 1][:, 0], train_x[train_y == 1][:, 1], 'o')
plt.show()

对应图如下：

image-20250313235534534

数据预处理

主要对数据进行一下标准化

1
2
3
4
5
6
7
8
9
10
11
# 计算平均值（两列要分别计算）
mu = train_x.mean(axis=0)
# 计算标准差（两列要分别计算）
sigma = train_x.std(axis=0)
# 定义标准化函数
def standardize(x):
    return (x - mu) / sigma

# 后续训练使用的，标准化后的数据
X = standardize(train_x)
y = train_y

开始训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 设置学习率
leaning_rate = 0.1
# 最大学习次数
max_epochs = 200

# 初始化权重和偏置
weights = np.random.randn(2) * 0.01
bias = 0

# 训练
for epoch in range(max_epochs):
    has_error = False
    for i in range(len(X)):
        # 计算预测值 z = x1w1 + x2w2 + b
        z = np.dot(X[i], weights) + bias
        # z >=0则预测为 1，否则预测为 0
        y_pred = 1 if z >= 0 else 0

        if y_pred != y[i]:
            # 预测错误，则更新权重和偏置(参考本文开始部分的公式)
            weights += leaning_rate * (y[i] - y_pred) * X[i]
            bias += leaning_rate * (y[i] - y_pred)
            has_error = True
    # 如果全部预测正确，可以提前结束
    if not has_error:
        break
    # 打印当前准确率，可以看到学习进度状态
    print(f"weights={weights}, bias={bias}")
    accuracy = np.mean([1 if np.dot(X[i], weights) + bias >= 0 else 0 for i in range(len(X))] == y)
    print(f"Epoch {epoch}, Accuracy: {accuracy}")

输出结果如下

1
2
3
4
5
6
weights=[0.16655886 0.06095784], bias=0.1
Epoch 0, Accuracy: 0.9024390243902439
weights=[0.16064312 0.14377813], bias=0.1
Epoch 1, Accuracy: 0.9512195121951219
weights=[0.26445705 0.25942353], bias=0.0
Epoch 2, Accuracy: 1.0

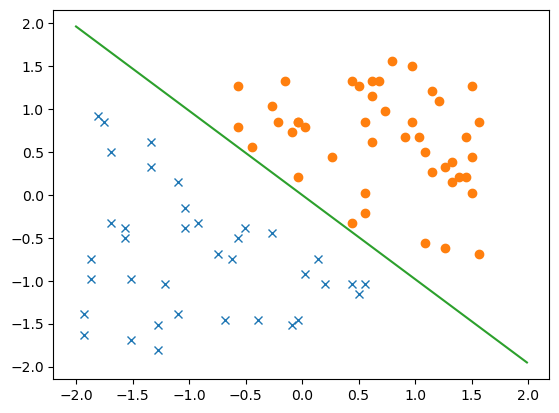
可以得到$0.26445705 x_1+0.25942353 x_2=0$，下面将这条分界线画出来

1
2
3
4
5
6
7
# 使用标准化后的数据进行绘制
plt.plot(X[y == 0][:, 0], X[y == 0][:, 1], 'x')
plt.plot(X[y == 1][:, 0], X[y == 1][:, 1], 'o')
# 生成数据，绘制对应数据计算后的值
xx = np.arange(-2, 2, 0.01)
plt.plot(xx, -weights[1] / weights[0] * xx)
plt.show()

对应结果

image-20250314002102327

此时预测函数可以如下定义

1
2
def predict(X):
    return np.dot(X, weights) + bias >= 0

最后我们再自己构造数据进行验证也查下

1
2
3
4
5
6
# 随意构造几个数据
data = [[60, 70], [80, 90], [50, 50], [70, 80]]
# 先对数据进行标准化(注意标准化公式中的参数，一定要使用训练时的均值和标准差)
stand_data = standardize(data)
# 进行预测
predict(stand_data)

输出结果如下，符合预期

1
> array([ True,  True, False,  True])